Métodos de Resolução do Solver

Como escolher qual o método de resolução a usar no Solver

O Solver do Microsoft Excel é uma ferramenta preciosa para resolver problemas de programação linear e não-linear, para encontrar soluções ótimas em problemas de pesquisa operacional. No entanto, é necessário ter cuidado quer na formulação do problema, quer na hora de o resolver com recurso ao Solver. 

A escolha do método de resolução a utilizar é fundamental para obter a melhor e mais rápida solução do nosso problema de otimização. 

A partir da versão 2010 do Excel, existem três algoritmos de resolução disponíveis na caixa "Selec. Método Resolução": o método LP Simplex, o método GRG Nonlinear e o método Evolutionary.

Então, qual dos métodos de resolução do Solver escolher? Para fazer a escolha do método de resolução mais apropriado é necessário ter em atenção ao problema que se pretende resolver e ao tipo de funções que estão envolvidas nas células da função objetivo e nas células das restrições.

E isto depende do tipo de problema que se pretende resolver, se é linear ou não linear, se tem restrições complexas, se a função objetivo tem descontinuidades, etc.

Quando usar o Método GRG Nonlinear? 

O método GRG Nonlinear (Generalized Reduced Gradient) é um algoritmo de resolução de problemas utilizado no Solver do Microsoft Excel para encontrar soluções ótimas para problemas de programação não-linear. Ele é utilizado quando a função objetivo e as restrições resultam de funções não lineares das variáveis de decisão e ainda com operações matemáticas que envolvem potências, cálculo exponencial ou trigonométrico.

Este algoritmo de otimização foi desenvolvido pelo Professor Leon Lasdon da Universidade do Texas e pelo Professor Allan Waren da Universidade de Cleveland. 

O método GRG Nonlinear é baseado no método de gradiente reduzido, que é uma técnica de otimização que utiliza a derivada da função objetivo para encontrar a direção de melhoria e, em seguida, atualiza as variáveis de decisão na direção de melhoria. 

O GRG foi desenvolvido para lidar com problemas não-lineares que não podem ser resolvidos pelo método LP Simplex, que é o algoritmo padrão utilizado para problemas lineares.

Uma das principais vantagens do método GRG Nonlinear é que ele é capaz de lidar com problemas não-lineares que possuem restrições não-lineares e funções objetivo não-lineares. Ele também é capaz de lidar com problemas que possuem restrições de igualdade e desigualdade. 

Além disso, o GRG é capaz de encontrar soluções ótimas para problemas que possuem múltiplos pontos ótimos.

De qualquer modo, o método GRG Nonlinear também tem suas desvantagens. Ele pode ser mais lento do que o método LP Simplex para problemas lineares e pode ter dificuldade em encontrar soluções ótimas para problemas não-lineares que possuem restrições muito complexas. Além disso, o GRG lida mal com problemas que possuem restrições de inteiro ou binário.

Quando usar o Método LP Simplex? 

O Método LP Simplex (linear Programming Simplex) é utilizado quando o objetivo e as restrições são funções lineares das variáveis de decisão. Ele é o algoritmo ideal para problemas de programação linear e programação com inteiros.

 

O método Simplex LP é um algoritmo de resolução de problemas utilizado no Solver do Microsoft Excel para encontrar soluções ótimas para problemas de programação linear. Este algoritmo deve ser utilizado quando a função objetivo e as restrições são funções lineares das variáveis de decisão, ou seja, quando o declive é constante. Este é o algoritmo padrão utilizado para problemas de otimização linear.

O método LP Simplex é baseado no algoritmo do método Simplex, que é uma técnica de otimização que utiliza a análise de tabelas para encontrar a solução ótima de um problema de programação linear. Ele funciona iterando através de diferentes soluções possíveis, até encontrar a solução ótima. O método LP Simplex é o algoritmo de resolução mais amplamente utilizado para problemas de programação linear e é conhecido por ser muito eficiente em termos de tempo de processamento.

Uma das principais vantagens do LP Simplex é que ele é capaz de lidar com problemas lineares de forma eficiente e é capaz de encontrar soluções ótimas para problemas que possuem múltiplos pontos ótimos. Além disso, ele é capaz de lidar com problemas que possuem restrições de igualdade e desigualdade.

No entanto, o LP Simplex também tem as suas desvantagens. Ele não é capaz de lidar com problemas não-lineares e não é capaz de lidar com problemas que possuem restrições de inteiro ou binário. Ele também pode ter dificuldade em encontrar soluções ótimas para problemas que possuem restrições muito complexas.

Quando usar o Método Evolutionary? 

Por fim, o método Evolutionary é um algoritmo de resolução de problemas utilizado no Solver do Microsoft Excel para encontrar soluções ótimas para problemas de programação não-linear. Ele é utilizado quando a célula objetivo e as células de restrições são determinadas a partir de funções cujos resultados variam de forma abrupta. 

Isto acontece geralmente quando nas células da função objetivo ou nas células das restrições são usadas fórmulas do tipo condicional (IF, SUMIF, etc.) tal como acontece com se utilizam fundação contendo ABS, MIN ou MAX para calcular o valor da célula objetivo ou de restrições, nestes casos o declive da função objetivo varia radicalmente para pequenas variações das variáveis de decisão, assim como o resultado. Para resolver problemas deste tipo utiliza-se o algoritmo Evolutionary.

O Evolutionary é baseado na técnica de algoritmos evolutivos, que é uma técnica de otimização inspirada em princípios da evolução biológica, como seleção natural, reprodução e mutação. Este método está projetado para lidar com problemas não-lineares e não-diferenciáveis que são difíceis de ser resolvidos por outros algoritmos.

Uma das principais vantagens do Evolutionary é que ele é capaz de lidar com problemas não-lineares e não-diferenciáveis que são difíceis de ser resolvidos por outros algoritmos. Ele também é capaz de encontrar soluções ótimas para problemas que possuem múltiplos pontos ótimos. Além disso, o Evolutionary é capaz de lidar com problemas que possuem restrições de inteiro ou binário.

Tal como os outros, o método Evolutionary também tem as suas desvantagens. Ele pode ser bastante mais lento do que os outros algoritmos para problemas não-lineares e não-diferenciáveis e pode ter dificuldade em encontrar soluções ótimas para problemas que possuem restrições muito complexas. Além disso, o Evolutionary tem dificuldade em lidar bem com problemas que possuem restrições de igualdade e desigualdade.

Como melhorar a resolução do método selecionado? 

Para a análise de problemas mais complexos, depois de selecionado o método de resolução, podem definir-se algumas opções a partir do botão “Opções” de modo a facilitar a sua resolução. Ao clicar no botão é exibida uma nova caixa de diálogo com três separadores:

No primeiro separador, podem definir-se opções comuns aos três algoritmos de resolução, onde estão disponíveis as seguintes opções:

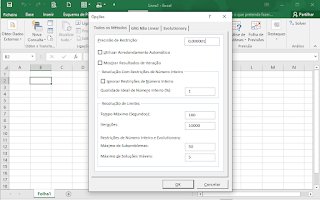
• Precisão de Restrição: aqui define-se qual o nível de tolerância a aplicar às restrições. Por exemplo, com um nível de precisão definido como 0,00001 a restrição C2>=1 poderá aceitar como válido um valor de C2 igual a 0,99999.

• Utilizar Arredondamento Automático: quando esta opção está ativa o Solver terá mais facilidade em resolver problemas em que a escala da variável objetivo e restrições são muito diferentes. Por exemplo, num problema em que o resultado da função objetivo é medido em quilómetros e as restrições variam na ordem dos milímetros, ativar esta opção levará ao redimensionamento interno das variáveis de modo a torna-las mais próximas, o que irá facilitar os cálculos internos, e consequentemente a melhores soluções na maior parte dos casos.

• Mostrar Resultados de Iteração: com esta opção ativa, os resultados são apresentados a cada iteração realizada pelo Solver. No canto inferior esquerdo da janela da folha de cálculo aparece o número da interação e o resultado da célula objetivo. Para aceitar, clicar em “Parar” e para continuar para a próxima iteração, clicar em “Continuar”.

• Ignorar Restrições de número Inteiro: com esta opção ativa, o Solver irá ignorar as restrições com números inteiros, binários ou todos diferentes, sendo possível definir a percentagem de tolerância (que por defeito é igual a 1%) do desvio em relação à solução ótima. Naturalmente, quanto maior for o desvio aceitável em relação à solução ótima, mais rápida será a resolução do problema. Em alguns casos, permitir um desvio de 1% a 2% representa uma poupança significativa no tempo de resolução.

No segundo separador, podem ser definidas as opções para o método de resolução GRG Não Linear, onde estão disponíveis as seguintes opções:

• Convergência: aqui define o valor máximo de variação do resultado das últimas cinco iterações antes de o Solver terminar a resolução do problema. Quanto mais baixo for este valor maior será a precisão da solução e consequentemente maior será o tempo que levará até encontrar a uma solução. Por isso, este fator deve ser escolhido ponderadamente por um lado para não afetar a solução e por outro lado para não ampliar exageradamente o tempo de execução.

• Derivadas: define o método de diferenciação utilizado no algoritmo. A opção “Adiantada” é a escolha por defeito, no entanto, a opção “Central” é a mais precisa embora seja necessário realizar o dobro dos cálculos a cada iteração e consequentemente mais tempo para obtenção de uma solução. 

• Utilizar Multistart: com esta opção ativada, o método GRG Não Linear é executado várias vezes testando diferentes valores iniciais para as variáveis de decisão. Esta opção permite chegar a resultados mais precisos, no entanto, requer mais tempo de processamento.

• Tamanho da População: define-se o número de pontos de partida das variáveis de decisão, valor que pode variar entre 10 e 200.

• Seed Aleatório: aqui indica-se um número aleatório positivo e inteiro que define o gerador de pontos de partida das variáveis de decisão. Se nada for indicado o Solver utilizará pontos de partida diferentes a cada resolução. 

• Exigir Limites em Variáveis: ao selecionar esta opção as variáveis de decisão serão restringidas entre um limite inferior e um limite superior. Neste caso, o método de resolução será mais eficaz.

Por fim, no terceiro separador permite definir diversas opções para o método Evolutionary, estando definidas as seguintes opções:

• Convergência: define o valor máximo de variação percentual permitida, a cada iteração, para os valores da célula objetivo antes de terminar a resolução do problema. Tal como no método GRG, quanto mais baixo for este valor mais precisa será a solução encontrada e mais tempo será necessário para a convergência.

• Taxa de Mutação: define o valor da frequência relativa que qualquer uma das células das variáveis de decisão pode variar para gerar uma nova iteração. Este valor será definido entre 0 e 1 e quanto maior for, maior será a probabilidade de encontrar uma solução ótima, do mesmo modo que mais lento será o processo de resolução do problema.

• Tamanho da População: permite definir um valor entre 10 e 200 que determina o número de valores diferentes das variáveis de decisão usados a qualquer momento durante a resolução do problema.

• Seed Aleatório: define um valor positivo e inteiro que fixa o valor dos pontos de partida das variáveis de decisão. Quando deixado em branco será usado um número aleatório diferente cada vez que se executa o Solver.

• Tempo Máximo Sem Melhoramento: é o tempo máximo de execução permitido, medido em segundos, sem que a solução do problema apresente melhorias.

• Exigir Limites em Variáveis: se está opção estiver ativa, no modelo as variáveis de decisão deverão estar restringidas por limites inferiores e limites superiores.

Considerações sobre a escolha do Algoritmo de resolução do Solver

Em resumo, os algoritmos de resolução de problemas disponíveis no Solver do Excel incluem o método LP Simplex, o método GRG Não Linear e o método Evolutionary. Cada um destes algoritmos tem as suas próprias vantagens e desvantagens e é importante escolher o algoritmo adequado para o problema específico que se pretende analisar. Além de escolher o algoritmo de resolução de problemas adequado, é importante definir criteriosamente algumas opções a partir do botão "Opções" para facilitar a resolução do problema. 

Por exemplo, a opção a "Precisão das Restrições" define o nível de tolerância aplicado às restrições, enquanto a opção "Utilizar Arredondamento Automático" facilita a resolução de problemas em que a escala da variável objetivo e restrições são muito diferentes. 

A opção "Mostrar Resultados de Iteração" permite ver os resultados de cada iteração realizada pelo Solver, o que pode ser útil para ir acompanhando o processo de convergência.

Em geral, é importante lembrar que escolher o algoritmo de resolução de problemas adequado e definir as opções corretas é apenas uma parte da solução para um problema de otimização. 

A modelação do problema, a análise de sensibilidade e a verificação do preço sombra também são importantes para garantir que a solução encontrada seja viável e aplicável para a situação real em concreto.

Espero ter ajudado porque, de acordo com o Google, todos os dias há centenas de pessoas como você a pesquisar qual o método de resolução utilizar no Solver, bem como definir as várias opções em cada método. 

A ferramenta Solver Excel tem três algoritmos de resolução de problemas de otimização e agora você já pode usá-los com maior conhecimento.

E você, achou este artigo útil? foi fácil entender como escolher o método de resolução mais adequado? Então, por favor, partilhe esta informação nas redes sociais abaixo para ajudar mais pessoas a encontrar uma resposta para aquilo que procuram sobre Solver no Excel.